大家一定都喝过汽水，汽水中常常有许多小小的气泡，哗啦哗啦飘到上面来。这是因为组成小气泡的二氧化碳比水要轻，所以小气泡可以一点一点向上浮动。

而我们的冒泡排序之所以叫做冒泡排序，正是因为这种排序算法的每一个元素都可以像小气泡一样，根据自身大小，一点一点向着数组的一侧移动。

时间复杂度：最好 O(n) 最坏O(n²)

1.1. 原理

比较两个相邻的元素，将值大的元素交换至右端。

1.2. 思路

依次比较相邻的两个数，将小数放在前面，大数放在后面。即在第一趟：首先比较第1个和第2个数，将小数放前，大数放后。然后比较第2个数和第3个数，将小数放前，大数放后，如此继续，直至比较最后两个数，将小数放前，大数放后。

第一趟比较完成后，最后一个数一定是数组中最大的一个数，所以第二趟比较的时候最后一个数不参与比较；

第二趟比较完成后，倒数第二个数也一定是数组中第二大的数，所以第三趟比较的时候最后两个数不参与比较；

依次类推，每一趟比较次数-1；

……

具体如何来移动呢？让我们来看一个栗子：

有8个数组成一个无序数列：5，8，6，3，9，2，1，7，希望从小到大排序。

按照冒泡排序的思想，我们要把相邻的元素两两比较，根据大小来交换元素的位置，过程如下：

首先让5和8比较，发现5比8要小，因此元素位置不变。

接下来让8和6比较，发现8比6要大，所以8和6交换位置。

继续让8和3比较，发现8比3要大，所以8和3交换位置。

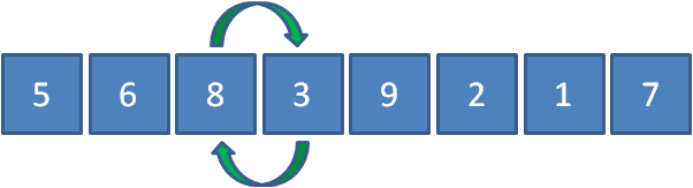
继续让8和9比较，发现8比9要小，所以元素位置不变。

接下来让9和2比较，发现9比2要大，所以9和2交换位置。

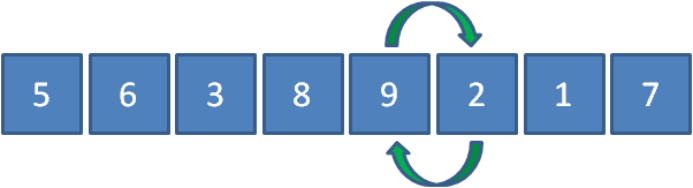
接下来让9和1比较，发现9比1要大，所以9和1交换位置。

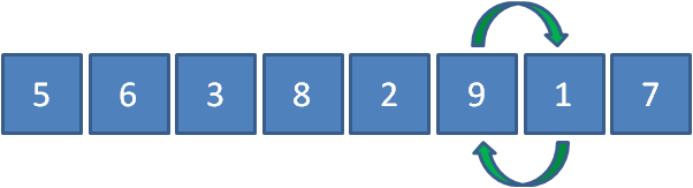
最后让9和7比较，发现9比7要大，所以9和7交换位置。

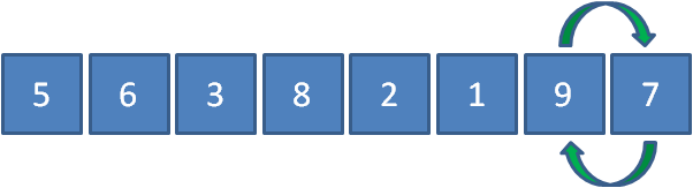
这样一来，元素9作为数列的最大元素，就像是汽水里的小气泡一样漂啊漂，漂到了最右侧。

这时候，我们的冒泡排序的第一轮结束了。数列最右侧的元素9可以认为是一个有序区域，有序区域目前只有一个元素。

至于后续的交换细节，我们这里就不详细描述了，第二轮过后的状态如下：

第三轮过后的状态如下：

第四轮过后状态如下：

第五轮过后状态如下：

第六轮过后状态如下：

第七轮过后状态如下（已经是有序了，所以没有改变）：

第八轮过后状态如下（同样没有改变）：

到此为止，所有元素都是有序的了，这就是冒泡排序的整体思路。

由此可见：N个数字要排序完成，总共进行N-1趟排序，每i趟的排序次数为(N-1-i)次，所以可以用双重循环语句，外层控制循环多少趟，内层控制每一趟的循环次数，即

for(int i=0;i<arr.length-1;i++){
    for(int j=0;j<arr.length-i-1;j++){
    //判断是否需要交换位置，是则交换
}

1.3. 完整代码

public class Main {
    
public static void main(String[] args) {
//定义数组
        
int[] num={1,5,3,8,4,9};
        
//第一层循环
        
for(int i=0;i<num.length-1;i++)
{
            
//第二层循环
            
for(int j=0;j<num.length-1;j++)
{
                
//判断第一个数是否比第二个数大
                
   if(num[j]>num[j+1])
   {
                    
//如果是则交换
                   
      int temp=num[j];
   num[j]=num[j+1];
   num[j+1]=temp;
   }
 }
}
        
 //输出
        
 System.out.println("排序后的数组为：");
        
 for(int i=0;i<num.length;i++)
 {
  System.out.println(num[i]);
 }
 }
}

缺点1：每一趟比较都要比较到数组的最后，没有必要，只要比较到无序数列最后即可

缺点2：不管是否有序，都要进行n-1趟循环；

优化后的代码：

public class Test {
public static void main(String[] args) {
   //定义数组
   int[] num={1,5,3,8,4,9};
   //第一层循环
   for(int i=0;i<num.length-1;i++)
   {
      boolean flag=true;
      //第二层循环
       for(int j=0;j<num.length-1-i;j++)
      {
         //判断第一个数是否比第二个数大
         if(num[j]>num[j+1])
         {
            //如果是则交换
            int temp=num[j];
            num[j]=num[j+1];
            num[j+1]=temp;
            =false;
          }
       }
       if(flag) {
         break;
       }
    }
    //输出
    System.out.println("排序后的数组为：");
    for(int i=0;i<num.length;i++)
    {
       System.out.println(num[i]);
    }
  }
}